Зубчатый вариатор с постоянным зацеплением колес. Теоретические основы создания

  

 

 

 

 

К.С.Иванов, доктор технических наук, профессор.

Казахский институт механики и машиноведения  им. акад. У.А.Джолдасбекова, Алматинский университет энергетики и связи. Алматы, Казахстан

 

Аннотация. Зубчатый вариатор – это зубчатый механизм с переменным передаточным отношением. Теория механизмов отрицает возможность существования зубчатого механизма с переменным передаточным отношением при постоянном зацеплении зубчатых колес. Создание зубчатого вариатора возможно только путем введения дополнительной степени свободы при сохранении определимости движения механизма. Такой механизм способен сначала разделить входной поток энергии на два независимых потока, а потом объединить разделенные потоки энергии в один выходной поток с переменным передаточным отношением. Для обеспечения принципиально новой технологии передачи энергии можно использовать зубчатый дифференциал и планетарный объединяющий механизм. Новая идея создания зубчатого механизма с переменным передаточным отношением соответствует ранее выполненным исследованиям о наличии силовой адаптации в механизме с двумя степенями свободы и с одним входом. Зубчатый вариатор в виде замкнутого дифференциального механизма с двумя степенями свободы будет не только иметь переменное передаточное отношение, но и адаптироваться к внешней нагрузке. Адаптивный передаточный механизм не нуждается в системе управления. Зубчатый вариатор является самонастраивающимся механизмом без системы управления. Новый принцип создания механизма с переменным передаточным отношением предопределяет абсолютную адекватность условиям работы и беспрецедентную простоту конструкции. Зубчатый вариатор открывает принципиально новую концепцию создания адаптивной техники для машин с переменным технологическим сопротивлением (например, адаптивных коробок передач).

В работе изложены основы теории зубчатого адаптивного вариатора.

Работа выполнена на основе законов механики.

Ключевые слова: Зубчатый вариатор, дифференциальный механизм, силовая адаптация.

ВВЕДЕНИЕ

Зубчатый вариатор, представляющий собой зубчатый механизм с постоянным зацеплением зубчатых колес и с переменным передаточным отношением, является мечтой конструкторов, создающих коробки передач автомобилей.

В настоящее время в качестве автоматических коробок передач автомобиля используются две разновидности агрегатов с переменным передаточным отношением: автомат и вариатор.

Автомат – это сложный механический агрегат, содержащий гидротрансформатор, многоступенчатый зубчатый механизм с фрикционными дисками, устройство переключения ступеней и систему управления. Автомат имеет громоздкую конструкцию, сложность управления и низкий КПД.

Вариатор – это клиноременный механизм с бесступенчатым регулированием передаточного отношения. В настоящее время существуют только фрикционные вариаторы (клиноременные, тороидные). Клиноременный вариатор содержит два диска с переменными управляемыми диаметрами,  клиновой металлический ремень и систему управления. Фрикционный вариатор имеет малую надежность и низкий КПД.

Зубчатый бесступенчатый вариатор с постоянным зацеплением зубчатых колес и заданным диапазоном передаточных отношений мог бы работать без гидротрансформатора и без потерь на трение. Зубчатый вариатор в отличие от фрикционного вариатора способен обеспечить надежную передачу усилия и высокий КПД.

В существующих агрегатах переменное передаточное отношение создается с помощью дифференциальной связи. Дифференциальная связь аналитически представляет собой уравнение взаимосвязи параметров, которое помимо геометрических параметров содержит относительные скорости движения [1]. В автомате дифференциальная связь обеспечивается гидравликой, во фрикционном  вариаторе – трением. Такая связь приводит к потерям энергии и снижению кпд.

Зубчатый вариатор с постоянным зацеплением зубчатых колес в обычном представлении не может иметь дифференциальной связи. Для создания зубчатого вариатора необходимо использовать принципиально новый подход к конструированию механизма. Принципиально новый подход к конструированию вариатора был найден интуитивно при анализе зубчатого дифференциального механизма. Как известно дифференциальный механизм может раскладывать движение входного звена на два независимых выходных движения двух выходных звеньев. Если затем объединить разделенные независимые потоки энергии, то объединенный выходной поток энергии приобретет некоторую независимость параметров. Создание зубчатого вариатора возможно только путем введения дополнительной степени свободы при сохранении определимости движения механизма. Механизм  вариатора должен сначала разделить входной поток энергии на два независимых потока, а потом объединить разделенные потоки энергии в один выходной поток с переменным передаточным отношением. Для обеспечения принципиально новой технологии передачи энергии можно использовать зубчатый дифференциал и планетарный объединяющий механизм.

Но такой механизм будет иметь две степени свободы, а по законам механики он должен быть неработоспособным [1, 2]. Новая идея создания зубчатого механизма с переменным передаточным отношением соответствует ранее выполненным исследованиям о наличии силовой адаптации в механизме с двумя степенями свободы и с одним входом [3, 4, 5].

Теоретическое описание закономерностей взаимосвязи параметров планетарного механизма с двумя степенями свободы, полученного указанным способом, привело к совершенно неожиданному результату – кинематическая цепь имеет определенность движения! Было доказано, что независимость движения выходного звена и определимость кинематической цепи с двумя степенями свободы может иметь место только в рассмотренном случае, когда объединение дифференциального и замыкающего механизмов образует кинематическую цепь с промежуточным подвижным замкнутым контуром, соединяющим входное и выходное звенья [3 – 6]. Последующие многочисленные теоретические разработки привели к теоретическому описанию принципиально нового явления в механике, которое было названо «Эффект силовой адаптации в механике» [7 - 10].

Зубчатый вариатор в виде замкнутого дифференциального механизма с двумя степенями свободы будет не только иметь переменное передаточное отношение, но и адаптироваться к внешней нагрузке. Адаптивный передаточный механизм не нуждается в системе управления. Зубчатый вариатор является самонастраивающимся механизмом без системы управления. Новый принцип создания механизма с переменным передаточным отношением предопределяет абсолютную адекватность условиям работы и беспрецедентную простоту конструкции.

На основе  научного открытия «Эффект силовой адаптации в механике» были разработаны патенты Казахстана, России и Германии с описанием принципиально новых адаптивных зубчатых вариаторов [11 - 15].

Теоретическое обоснование для создания адаптивных зубчатых вариаторов в виде механической бесступенчато регулируемой передачи было разработано в работах Иванова К.С. [16 - 18]. Было доказано, что кинематическая цепь с двумя степенями свободы, содержащая подвижный замкнутый контур, обладает принципиально новым свойством силовой адаптации к переменной нагрузке.   Кинематическая цепь с двумя степенями свободы и одним входом, содержащая замкнутый контур, под действием переменной выходной нагрузки самостоятельно изменяет выходную скорость движения. Такая кинематическая цепь была названа адаптивным механизмом.

Адаптивный вариатор  с постоянным зацеплением зубчатых колес позволяет передавать движение от двигателя постоянной мощности на выходной рабочий орган со скоростью, обратно пропорциональной технологической нагрузке. Открытие эффекта силовой адаптации позволило найти принципиально новые закономерности взаимодействия силовых и кинематических параметров кинематической цепи с двумя степенями свободы.  Эти закономерности позволяют эффективно использовать зубчатый вариатор в робототехнике, в ветротурбинных установках и в спортивной технике  [20 - 22].

В дальнейшем были выполнены экспериментальные исследования, подтвердившие наличие эффекта силовой адаптации в механизме с двумя степенями свободы и одним входом [23].

Принципиально новая особенность адаптивного зубчатого вариатора состоит в том, что он в отличие от автомата и  фрикционного вариатора работает самостоятельно без системы управления. Переменная внешняя нагрузка сама управляет выходной скоростью вариатора. Такой способ регулирования передаточного отношения можно было бы назвать самонастройкой, а адаптивный вариатор можно считать самонастраивающимся к переменной нагрузке механизмом.

Зубчатый вариатор имеет фантастические преимущества и перед фрикционным вариатором и перед автоматом. Главные преимущества зубчатого вариатора:

1. Беспрецедентная простота конструкции.

2. Полная адекватность к технологии работы.

3. Отсутствие системы управления.

4. Высочайшая надежность и долговечность.

Сопоставление конструкций коробки-автомата, фрикционного вариатора  и зубчатого вариатора может быть выполнено с помощью рис. 1, 2, 3, 4.

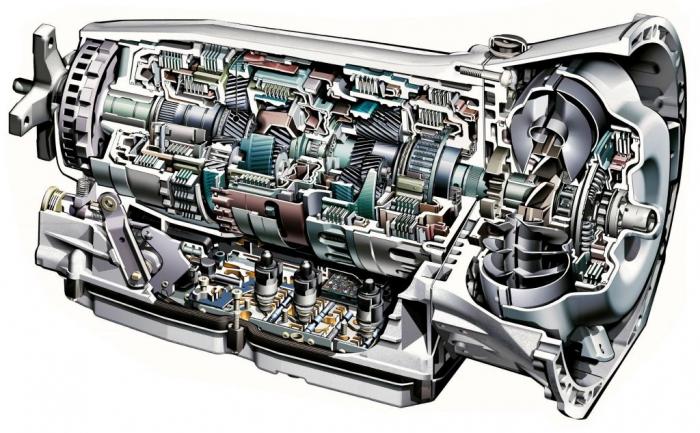
Рис. 1. Коробка передач автомат Mercedes-Benz

     

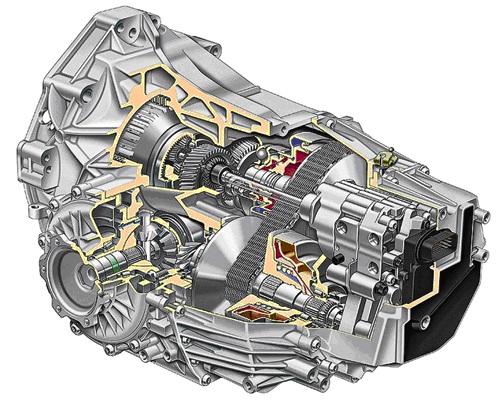
Рис. 2. Фрикционный вариатор Multitronic

 

 

 

                                                             

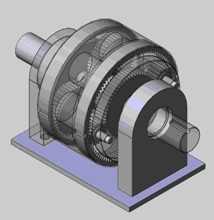
Рис. 3. Зубчатый вариатор

  

 

 

                                                             

Рис.4. Зубчатый вариатор (детали)

 

На фоне продолжающегося совершенствования громоздких конструкций автомата и вариатора, созданных на отживших принципах использования «жесткой» механики с одной степенью свободы, прогрессивные схемы и преимущества зубчатого двух подвижного вариатора кажутся просто фантастическими, неправдоподобными. Поэтому многочисленные публикации в прогрессивной мировой прессе об адаптивных зубчатых вариаторах с двумя степенями свободы остаются вне поля зрения практических разработчиков современных коробок передач. Использование устаревшей концепции создания автоматических коробок передач приводит к появлению все новых и новых усовершенствований изживших себя конструкций, к дальнейшему их усложнению, к всемерному использованию компьютерной техники для устранения врожденных дефектов морально устаревшей техники и в конечном итоге к снижению надежности и повышению стоимости коробок передач. Уже сейчас стоимость коробки передач (всего лишь передаточного механизма) сопоставима со стоимостью сложнейшего агрегата – двигателя.

Цель настоящей работы состоит в том, чтобы представить краткую теорию зубчатого вариатора на основе законов механики и общепринятых методик структурного, кинематического и динамического анализа механизмов, пригодную  для практической разработки высокоэффективных адаптивных коробок передач нового поколения.

 

1. Теоретические предпосылки создания зубчатого вариатора

Идея создания зубчатого вариатора основана на разделении и последующем объединении потока энергии. Разделение входного потока энергии выполняет разделяющий дифференциальный механизм с двумя степенями свободы и одним входом (рис. 5). Объединение разделенных потоков энергии выполняет объединяющий планетарный механизм с двумя входами и одним выходом (рис. 6).

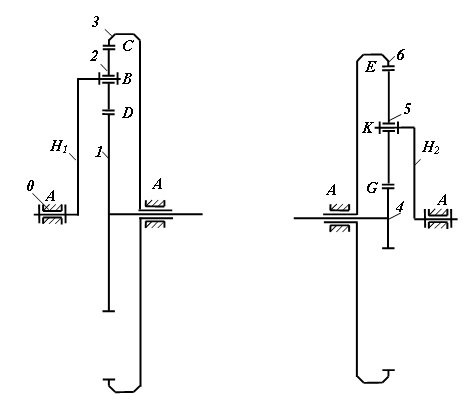
Рис. 5. Разделяющий механизм                Рис. 6. Объединяющий механизм  

 

Разделяющий механизм содержит стойку 0, входное водило H1, входной сателлит 2, выходное солнечное колесо 1 и выходное эпициклическое колесо 3. Кинематическая цепь имеет две степени свободы. Разделяющий механизм разделяет заданный входной поток мощности от водила H1  на колеса 1 и 3:

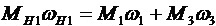.                                                  (1)

Здесь M- момент,  - угловая скорость.

Следует отметить, что моменты на колесах 1 и 3 должны содержать моменты сопротивления MR и моменты трения Mf:

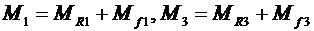,                            (2)

иначе колесо с большим моментом сопротивления окажется неподвижным.

 

Объединяющий механизм содержит стойку 0, входное солнечное колесо 4, входное эпициклическое колесо 6,  выходной сателлит 5 и выходное водило H2. Кинематическая цепь имеет две степени свободы.

Объединяющий механизм объединяет входные потоки мощности от колес 4 и 6 в поток мощности на выходном водиле H2:

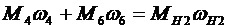     .                                                      (3)

Заданному выходному потоку мощности соответствуют вполне определенные входные потоки мощности.

Моменты на колесах 4 и 6 содержат движущие моменты  и моменты MD трения Mf:

 

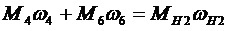.                                                          (4)

Создадим общий механизм, объединив колеса 1 и 4 в блок колес 1-4 и колеса 3 и 6 – в блок колес 3-6 (рис. 7).

В полученном механизме разделенные силовые потоки должны соответствовать входным силовым потокам объединяющего механизма, создающим заданный выходной силовой поток, а внутренние силовые потоки на блоках колес 1-4 и 3-6 должны оказаться уравновешенными.

 

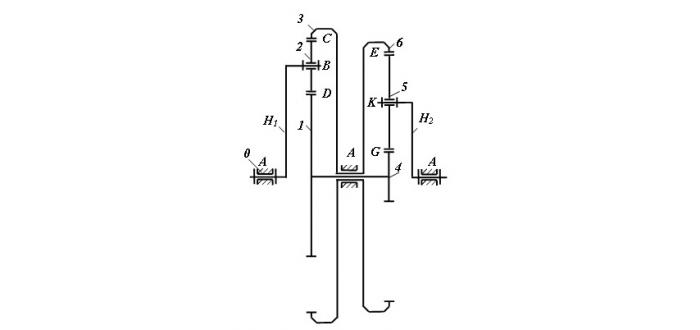
Рис. 7. Зубчатый вариатор

Выполним теоретическую проверку нашего предположения. Сложим уравнения (1) и (3) для получения уравнения взаимосвязи параметров общего механизма. При этом будем учитывать

 

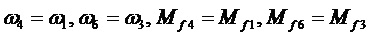.                                    (5)

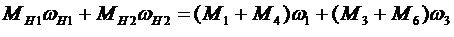.                 (6)

Здесь          .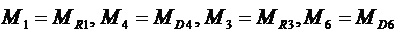

После подстановки этих значений (2), (4)  и (5) в уравнения (1) и (3) окажется, что моменты трения в уравнение (6) не входят.

Левая часть уравнения (6) определяет сумму мощностей внешних сил.

Правая часть уравнения (6) определяет сумму мощностей внутренних сил.

Будем использовать предположение, что рассматриваемая кинематическая цепь имеет идеальные связи. Тогда сумма мощностей (или работ) внутренних сил равна нулю

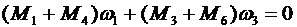.                                   (7)

То есть имеет место равновесие внутренних сил по принципу виртуальных перемещений или определимость движения (с учетом принятия действительных перемещений за виртуальные).

Из уравнения (6) получим

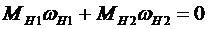.                                                      (8)

То есть сумма мощностей (или работ) внешних сил равна нулю. Имеет место равновесие по принципу виртуальных перемещений или определимость движения.

Особенность структуры созданного механизма состоит в том, что он содержит входное водило, выходное водило и размещенный между ними подвижный замкнутый контур из колес 1-2-3-6-5-4.

Итак, рассмотренный принцип создания механизма приводит к следующим важнейшим результатам:

1) Кинематическая цепь с двумя степенями свободы, имеющая только один вход обладает определимостью движения (является механизмом)!

2) Полученный механизм обладает принципиально новым свойством - свойством силовой адаптации! Это свойство с учетом направлений моментов следует из формулы (8)

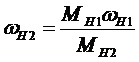.                                                                     (9)

При заданной постоянной входной мощности выходная угловая скорость находится в обратной пропорциональной зависимости от выходного момента сопротивления.

Найденная закономерность является научным открытием в области механики, названным «Эффект силовой адаптации».

Механизм двумя степенями свободы и одним входом, содержащий подвижный замкнутый контур, будем называть адаптивным механизмом. Адаптивный зубчатый механизм является зубчатым вариатором с постоянным зацеплением зубчатых колес. Зубчатый адаптивный вариатор не только обеспечивает переменное передаточное отношение, но и  приводит это передаточное отношение в соответствие к требуемой   переменной нагрузке. То есть зубчатый адаптивный вариатор работает без системы управления. Он просто самостоятельно приспосабливается к переменной нагрузке.

Рассмотрим далее основные теоретические закономерности зубчатого адаптивного вариатора.

 

2. Принцип построения схемы зубчатого вариатора

Объектом исследования является адаптивный зубчатый вариатор с дифференциальной связью в виде уравнения (9). Адаптивный вариатор с дифференциальной связью имеет две степени свободы и только одно входное (начальное) звено.

В теоретической механике для определимой по положению механической системы используется условие равенства числа степеней свободы числу обобщенных координат [1]. Согласно этому условию в теории вариаторов и машин используется концепция построения плоских механизмов по принципу Ассура [2]. По этой концепции число начальных (или входных) звеньев механизма должно быть равно числу степеней свободы, а выходным звеном является звено структурной группы с нулевой подвижностью (группы Ассура). Однако теоретически возможна иная концепция построения механизма, при которой выходное звено аналогично входному звену присоединено к стойке и не принадлежит группе Ассура, а сама группа Ассура используется как промежуточная передаточная цепь между входным и выходным звеньями. Такая концепция построения вариатора в общем случае приводит к появлению дополнительной степени свободы и к потере кинематической определимости цепи. Однако если структура вариатора обеспечивает появление дополнительной связи, выраженной аналитически, определимость кинематической цепи будет иметь место. Ранее выполненные исследования показали, что структурная группа в виде замкнутого четырехзвенного контура накладывает дополнительную связь на движение звеньев [5, 7, 10] при отсутствии энергетических потерь и к определимости кинематической цепи с двумя степенями свободы при наличии только одного входа.

Адаптивный вариатор содержит геометрические связи и наложенную дифференциальную связь, обеспечивающую относительное движение звеньев под действием сил и силовую адаптацию к переменной внешней нагрузке.

Обычная дифференциальная связь между звеньями обеспечивает связь геометрических и кинематических параметров [1]. Она может быть обеспечена с помощью фрикционного, гидродинамического или электромагнитного адаптирующего эффекта. Получила широкое распространение дифференциальная связь с использованием гидродинамического адаптирующего эффекта в гидродинамической передаче автомобиля. Основное отличие дифференциальной связи от геометрической состоит в отсутствии жесткой связи между звеньями, что обеспечивает их относительное движение и позволяет получить переменное передаточное отношение.

Дифференциальная связь в адаптивном вариаторе создается подвижным замкнутым контуром [5, 10]. Такая дифференциальная связь ранее никогда не рассматривалась и не использовалась. Принципиально новая дифференциальная связь представляет собой уравнение взаимосвязи силового и кинематического параметров. Подвижный замкнутый контур обеспечивает адаптацию вариатора к переменной нагрузке на выходном звене за счет изменения его скорости движения. Вариатор с двумя степенями свободы, содержащий одно входное звено и подвижный замкнутый контур, реализует эффект силовой адаптации.

В настоящее время  выполнены научные исследования адаптивных механизмов, которые обеспечивают самонастройку к внешней нагрузке. Адаптивный передаточный механизм  обеспечивает передачу движения от двигателя постоянной мощности на рабочий орган со скоростью, обратно пропорциональной нагрузке. Адаптивный механизм обладает свойством механической адаптации. Механическая адаптация - это способность механизма самостоятельно без какой-либо системы управления приспосабливаться к переменной технологической нагрузке. Функциональная сущность адаптивного механизма – это обеспечение оптимального переменного передаточного отношения при постоянной мощности двигателя. Эта функция принципиально отличается от функции коробки передач, имеющей несколько ступеней, так как при использовании ступенчатой коробки передач на каждой ступени необходимо изменять мощность двигателя для достижения оптимального результата при передаче энергии. В отличие от ступенчатой коробки передач адаптивный передаточный механизм обеспечивает принципиально новое явление в технике – самонастройку к переменной технологической нагрузке при постоянной мощности двигателя без использования системы управления. Адаптивный передаточный механизм принципиально отличается от вариатора отсутствием системы управления. Таким образом, адаптивный механизм можно считать самонастраивающимся к переменной нагрузке механизмом.

Адаптивный зубчатый вариатор имеет вид замкнутого зубчатого дифференциала с двумя степенями свободы (рис. 7). Он содержит стойку 0, водило H1, замкнутый четырехзвенный контур из зубчатых колес 1-2-3-6-5-4 и водило H2. Солнечные колеса 1, 4 объединены в блок колес 1-4. Эпициклические колеса 3, 6 объединены в блок колес 3-6.

Кинематическая цепь имеет две степени свободы.

Особенности кинематической цепи:

1) Цепь имеет два внешних звена (водила H1  и H2 ), которые соединены структурной группой с нулевой подвижностью 1-2-3-6-5-4. Эта структурная группа представляет собой замкнутый четырехзвенный контур.

2) Мгновенные центры скоростей центральных зубчатых колес совпадают (расположены на центральной оси зубчатого дифференциала).

 

3. Структура зубчатого вариатора

Структура зубчатого вариатора (рис. 7) принципиально отличается от структуры многоступенчатого передаточного механизма. Зубчатый механизм с двумя степенями свободы имеет два внешних звена (водила H1  и H2 ) и размещенную между ними структурную группу Ассура с нулевой подвижностью. Эта структурная группа представляет собой замкнутый четырехзвенный контур из зубчатых колес 1-2-3-6-5-4.

Число степеней свободы кинематической цепи определяем по формуле Чебышева

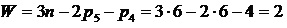                                                    .                                     (10)

Как было отмечено выше, зубчатый вариатор может работать в режиме с двумя степенями свободы и в режиме с одной степенью свободы в зависимости от величины выходной нагрузки.

 

4. Работа зубчатого вариатора

Зубчатый вариатор может работать в режиме с двумя степенями свободы и в режиме с одной         степенью свободы.

Движение механизма с двумя степенями свободы имеет место в эксплуатационном режиме движения с саморегулированием.

Движение с одной степенью свободы имеет место в двух случаях:

1) При пуске вариатора, когда выходное водило остановлено.

2) При перегрузке, когда момент сопротивления на выходном водиле превышает максимальное значение, что также приводит к остановке выходного водила.

Рассмотрим сначала пуск вариатора.

Вариатор, размещенный между двигателем и рабочим органом машины, допускает пуск с постепенным увеличением момента сопротивления (с использованием муфты сцепления) и с прямым воздействием на рабочий орган (без использования муфты сцепления).

Муфта сцепления должна быть размещена после выходного вала вариатора. Начало пуска происходит при отключенном рабочем органе. Механизм вариатора при отсутствии выходной нагрузки переходит в движение с одной степенью свободы при вращающемся выходном водиле. Угловые скорости всех звеньев одинаковы и равны входной угловой скорости. Контур из зубчатых колес вращается как одно целое при отсутствии относительного движения колес внутри контура. Момент сопротивления на выходном водиле может иметь место при действии инерционных сил, или при наличии внутреннего трения. Максимально возможный момент сопротивления на выходном водиле равен входному движущему моменту.

После  соединения вариатора с рабочим органом (с помощью муфты сцепления) механизм вариатора переходит в эксплуатационный режим движения. Начинается движение с двумя степенями свободы при наличии относительного движения зубчатых колес внутри замкнутого контура. Увеличение выходного момента сопротивления приводит к уменьшению выходной угловой скорости и к троганию с места. После трогания с места начинается эксплуатационный режим движения с наличием эффекта силовой адаптации.

Пуск вариатора при отсутствии муфты сцепления происходит при неподвижном выходном водиле. Трогание с места выходного водила может иметь место при наличии внутреннего момента сопротивления в замкнутом контуре, который может быть представлен в виде некоторого приведенного момента сопротивления MR5 на выходном сателлите 5. Момент сопротивления MR5 имеет место как инерционный момент или как момент сил трения. В момент трогания с места максимально возможный момент сопротивления на выходном водиле равен входному движущему моменту. Поэтому пуск должен происходить в режиме увеличения мощности двигателя. После трогания с места выходного водила начинается эксплуатационный режим движения с наличием эффекта силовой адаптации.

Рассмотрим работу вариатора при перегрузке.

Когда момент сопротивления на выходном водиле превышает максимальное значение, происходит остановка выходного водила. Двигатель продолжает работать при неподвижном рабочем органе. Режим работы при работающем двигателе и остановленном рабочем органе можно назвать стоповым режимом движения. Возможность перехода вариатора в стоповый режим движения имеет важное практическое значение. Стоповый режим движения позволяет предотвратить выход механизма из строя при перегрузках.

После устранения перегрузки механизм продолжит работу в эксплуатационном режиме движения.

 

5. Кинематический анализ зубчатого вариатора

Зубчатый вариатор представляет собой кинематическую цепь с двумя степенями свободы. Поэтому кинематический анализ вариатора состоит в определении скоростей всех точек механизма по заданным скоростям двух внешних звеньев. Удобно выполнять кинематический анализ вариатора с помощью картины скоростей (рис. 8).

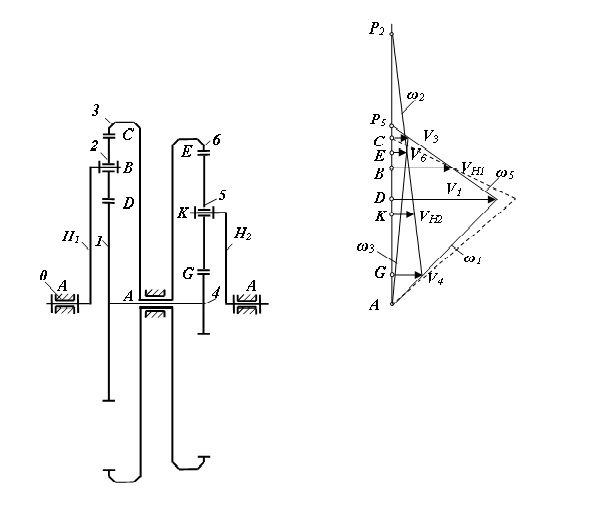
Рис. 8. Зубчатый вариатор с двумя степенями свободы и картина его скоростей

 

На картине скоростей представлены линейные скорости Vi точек механизма в виде горизонтальных линий и угловые скорости звеньев i   - в виде наклонных линий.

 

Угловые скорости 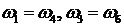 промежуточных звеньев 1-4 и 3-6 определяются через известные угловые скорости внешних звеньев, водил  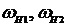и передаточные отношения при остановленных водилах.

Передаточные отношения звеньев передачи будем определять через числа зубьев колес Zi,               i = 1, 2,..., 6.  Взаимосвязь угловых скоростей механизма определяется формулами

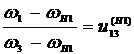                                                                       ,                                                      (11)

 

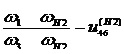                                                                                                                                 (12)

 

где ,,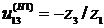 

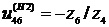
Из (11)

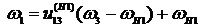                                                                                                                (13)

Из (12)

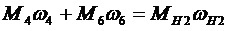                                                                                                      (14)

Вычтем (14) из (13), получим

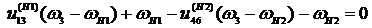. Отсюда

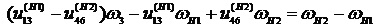, откуда

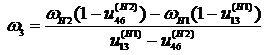.                                                                                                  (15)

Формулы (15) и (14) определяют последовательность действий по определению угловых скоростей 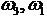 звеньев передачи.

Угловая скорость сателлита 2 определяется из условия 

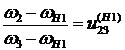                                                                    ,                                                             (16)

где 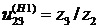. Отсюда

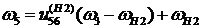                                                                                                               (17)

Угловая скорость сателлита 5 определяется из условия 

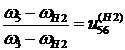                                                                    ,                                                             (18)

где 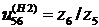. Отсюда

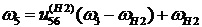                                                                     .                                         (19)

Следует отметить, что при отсутствии подвижности внутри контура кинематическая цепь будет двигаться в состоянии с одной степенью свободы. В этом случае угловые скорости всех звеньев одинаковы.

Таким образом, все кинематические и силовые параметры определены, и весь механизм имеет кинематическую и статическую определимость.

 

6. Силовой анализ зубчатого вариатора

Выполним силовой анализ кинематической цепи (рис. 8) по общепринятой методике. Задача силового анализа механизма с двумя степенями свободы состоит в определении реакций в кинематических парах и в определении обобщенных сил на двух внешних звеньях.

Некоторые особенности действия сил имеют место для рассматриваемой кинематической цепи. Будем считать, что на внешние звенья действуют обобщенные силы - моменты  MH1 и MH2 на водилах H1 и H2. На промежуточную структурную группу Ассура внешние силы не действуют (силами тяжести звеньев и силами инерции звеньев пренебрегаем из-за их малости по сравнению с силами на внешних водилах).

Силовой анализ следует начать с рассмотрения структурной группы 1-2-3-6-5-4 в виде замкнутого контура, состоящего из зубчатых колес. Структурная группа содержит блок солнечных колес 1-4, сателлит 2, блок эпициклических колес 3-6 и сателлит 5. Такая структурная группа ранее никогда не рассматривалась в силовом анализе механизмов. Однако для этой структурной группы можно составить условия равновесия статики,  которые определяют взаимосвязь внутренних и внешних сил. Будем считать, что внешними силами для рассматриваемой структурной группы является сила FH1, передаваемая со стороны водила H1  на точку B, и сила  FH2, передаваемая со стороны водила   H2 на точку K. Внутренними  силами являются реакции в кинематических парах в точках   C,E,D,G.

Первая особенность рассматриваемой структурной группы состоит в том, что все внутренние силы R32, R65, R12, R45 могут быть выражены по условиям статики через активные силы FH1 и FH2.

Для  звеньев контура 2 и 5 выразим реакции в кинематических парах D,C,G,E через внешние силы FH1, FH2, приложенные в точках B,K.

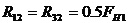                                                                        .                                                         (20)

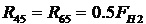 .                                                                                                                           (21)

Здесь,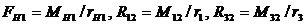 

            ,

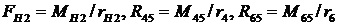MH1, MH2 - моменты на водилах,

rH1, rH2 - радиусы водил,

M12, M32 - моменты, создаваемые на сателлите 2 реакциями R12, R32 со стороны зубчатых колес 1 и 3,

M45, M65 - моменты, создаваемые на сателлите 5 реакциями R45, R65 со стороны зубчатых колес 4 и 6,

ri (i=1,2,....6) - радиусы колес.

После подстановки значений сил в уравнения (20), (21) получим  формулы для определения внутренних моментов через внешние моменты

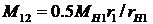                                                                                            ,                             (22) 

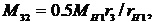                                                                                                                          (23)

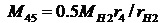                                                                                           ,                             (24)

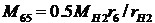                                                                                             .                             (25)    

Составим для сателлита 2 уравнение равновесия в виде суммы моментов относительно его мгновенного центра скоростей P2

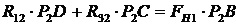                                                                            .                            (26)

Умножим уравнение (26) на 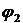 ( 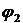- угол поворота звена 2 вокруг полюса P2), получим

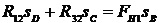                                                                               .                                           (27)

Составим для сателлита 5 уравнение равновесия в виде суммы моментов относительно его мгновенного центра скоростей  P5

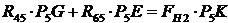                                                                                .                          (28)

Умножим уравнение (28) на 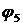 ( 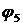- угол поворота звена 5 вокруг полюса P5), получим

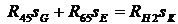                                                                                   .                                   (29)

 Здесь SB, SC, SD, SE,SG,SK – действительные перемещения точек B, C, D, E, G, K.                   

Выразим перемещения точек через мгновенные углы поворота звеньев относительно центральной оси механизма и радиусы: ,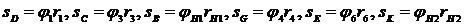

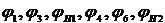 - мгновенные углы поворота зубчатых колес и водил.

Формулы (27), (29) определяют возможность преобразования уравнений моментов (26), (28) в уравнения равновесия по принципу возможных перемещений (27), (29) с использованием действительных перемещений вместо возможных.

Формулы (27), (29) соответствуют принципу возможных перемещений для всей кинематической цепи, поскольку мгновенные центры скоростей центральных зубчатых колес 1-4 и 3-6 совпадают с центральной осью механизма. 

С учетом 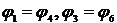 и времени получим

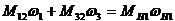                                                                          ,                                           (30)

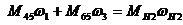                                                                         .                                          (31)

Так как сателлиты 2 и 5 входят в состав механизма в целом, сложим составленные выражения. Получим условие взаимодействия параметров кинематической цепи в целом

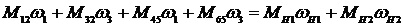                                                        .    (32)                           

В левой части уравнения (32) имеет место сумма мощностей (соответствующая сумме работ) внутренних сил контура.

В рассматриваемом механизме все внутренние силы определены через известные внешние силы, все внутренние перемещения определены через внешние перемещения.Следовательно, работа (или мощность) внутренних сил на возможных внутренних перемещениях определена. Связи в кинематических парах идеальные и стационарные. Работа внешних сил не может переходить в работу внутренних сил. Следовательно, работа (мощность) внутренних сил на возможных внутренних перемещениях равна нулю

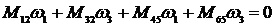                                                         .                                   (33)                       

Правая часть уравнения (22) представляет собой сумму мощностей (соответствующую сумме работ) внешних сил контура. При выполнении условия (23) получим из уравнения (22) условие равновесия для внешних сил согласно принципу возможных работ

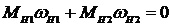                                                                        .                                              (34)

Приведенные зависимости позволяют определить все силовые параметры кинематической цепи, что свидетельствует о ее статической определимости.

Выполненный силовой анализ механизма с двумя степенями свободы позволяет сделать следующие выводы:

1) Уравнение статики (уравнение моментов) может быть преобразовано в уравнение равновесия по принципу возможных перемещений.

2) Рассматриваемая кинематическая цепь в виде дифференциального механизма с замкнутым контуром, содержащим зубчатые колеса, позволяет получить общее уравнение равновесия всей цепи в виде уравнения взаимосвязи силовых и кинематических параметров по принципу возможных перемещений.

3) Представляется возможным общее условие взаимосвязи силовых и кинематических параметров (32) представить в виде двух отдельных частей для внешних сил и для внутренних сил.

4) Полученное условие равновесия по принципу возможных перемещений для внутренних сил позволяет рассматривать кинематическую цепь как систему с идеальными связями, для которой сумма работ внутренних сил равна нулю (33).

5) Из предположения идеальности кинематической цепи следует, что сумма работ внешних сил также равна нулю (34), что предопределяет равномерное движение кинематической цепи.

6) Условие взаимосвязи внешних сил (34) предопределяет наличие работ с разными знаками на внешних звеньях цепи (водилах H1  и H2). Звено с наличием отрицательной работы не может быть входным звеном, так как действующая на нем сила является не движущей силой, а силой сопротивления.

Этот главный вывод приводит к необходимости считать рассматриваемую кинематическую цепь как цепь, содержащую только одно входное звено.

Приведенное заключение не изменяет статуса определимости рассматриваемой кинематической цепи. Поскольку кинематическая цепь остается определимой, ее следует считать механизмом с двумя степенями свободы, но только с одним входом. При этом кинематическая определимость цепи сохраняется, поскольку для выходного звена обобщенная координата (скорость) определяется из уравнения взаимосвязи внешних параметров (34). Будем считать входным звеном водило H1. Выходным звеном является водило  H2. Из уравнения (34) следует

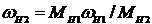                                                                              .                                             (35)

При этом внешние моменты остаются заданными, но MH1 - входной движущий момент, а MH2 - выходной момент сопротивления. Уравнение (35) выражает дополнительную связь, накладываемую контуром на движение звеньев цепи с двумя степенями свободы.

7) Дополнительная связь (35) обеспечивает эффект силовой адаптации к выходной нагрузке: при заданных постоянных параметрах входной мощности 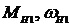 и заданном выходном моменте сопротивления MH2 выходная угловая скорость  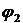находится в обратной пропорциональной зависимости от переменного выходного момента сопротивления MH2.

Формула (35) соответствует теореме о замкнутом контуре [4] – замкнутый контур обеспечивает силовую адаптацию к переменной нагрузке.

8) Условие взаимосвязи внутренних сил (33) предопределяет наличие работ с разными знаками на внутренних звеньях цепи.

Из уравнения (33) получим

  .

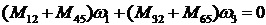С учетом знаков моментов (движущие моменты M12, M32, передаваемые со стороны входного сателлита 2, являются положительными,  моменты сопротивления M45, M65, передаваемые со стороны выходного сателлита 5, являются отрицательными) получим

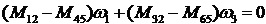                                                      .                                        (36)       

Уравнение (36) представляет собой уравнение работ (мощностей) на промежуточных звеньях 1-4 и 3-6. Уравнение (36) означает наличие равновесия на промежуточных звеньях 1-4 и 3-6 одновременно. В подвижном замкнутом контуре имеет место принципиально новая ситуация: равновесие в статике отдельно на каждом промежуточном звене отсутствует, но равновесие промежуточных звеньев одновременно в движении всего контура имеет место.

В замкнутом контуре имеет место циркуляция энергии.

Уравнение (36) содержит положительные и отрицательные члены и характеризует баланс мощностей на промежуточных звеньях контура.

Так как для рассматриваемой схемы, 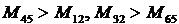, то из уравнения (36) получим

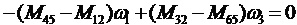                                                   .                                   (37)

 Отсюда

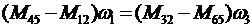                                                        .                                          (38)

Или .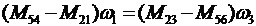

Обозначим .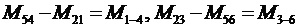

Здесь 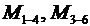 моменты на блоках колес 1-4 и 3-6. Тогда получим

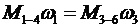                                                          .                                                                    (39)

Уравнение (39) отражает неизвестное ранее аналитическое выражение циркуляции энергии внутри контура во время его движения.

Таким образом, установлено, что зубчатый вариатор представляет собой замкнутый зубчатый дифференциальный механизм с двумя степенями свободы и с одним входом.

 

Заключение

Разработан принципиально новый подход к созданию схем механизмов с новыми свойствами. Новый подход предусматривает создание механизма с двумя степенями свободы, имеющего только один вход. Определимость движения механизма обеспечивает подвижный замкнутый контур, накладывающий дополнительную связь на движение звеньев. Структура механизма с двумя степенями свободы содержит входное звено, выходное звено и соединяющий эти звенья подвижный замкнутый контур в виде структурной группы с нулевой подвижностью. Механизм с двумя степенями свободы и с замкнутым контуром обладает свойством адаптации к переменной внешней нагрузке. Зубчатый механизм с двумя степенями свободы в виде замкнутого зубчатого дифференциала с подвижным замкнутым контуром является зубчатым адаптивным вариатором. Зубчатый адаптивный вариатор не только способен изменять передаточное отношение при постоянном зацеплении зубчатых колес, но и выполняет эту функцию автономно без использования механизма управления. Зубчатый адаптивный вариатор при постоянной входной мощности обеспечивает движение выходного вала со скоростью, обратно пропорциональной внешней нагрузке.

ОБ АВТОРЕ

Константин Самсонович Иванов,  доктор технических наук, Заведующий лабораторией Адаптивных механизмов,  главный научный сотрудник Институт Механики и машиноведения имени академика У.А. Джолдасбекова МОН РК, профессор кафедры «Системы управления аэрокосмической техникой»  Алматинского  университета энергетики и связи. Автор 4 монографий, более 480 изобретений, научных статей и докладов.  Член-корреспондент Национальной инженерной академии Казахстана.

Разработаны закономерности взаимосвязи параметров адаптивного вариатора как       кинематической цепи с идеальными связями в кинематике и в динамике на использовании законов  механики и методов теории механизмов и машин. Найденные закономерности определяют  принципиально новое научное направление:  исследование адаптивных механизмов с двумя  степенями свободы и с одним входом. Практическое значение найденных закономерностей огромно. Адаптивные вариаторы способны изменять передаточное отношение при постоянном зацеплении  зубчатых колес, являются простейшими по  конструкции, работают без механизмов управления,  имеют высочайшую надежность и эффективность  полностью адекватны условиям работы. Новое  поколение адаптивных механизмов вариаторов  способно совершить переворот в современной промышленности, особенно в автомобилестроении.

 

Список литературы

1.  Маркеев А.П. Теоретическая механика. - М., Наука. 1990. 414 с.

2.   Левитский Н.И. Теория механизмов и машин. - М., Наука. 1979. 576 с.

3.  Иванов К.С. Кинетостатика двухподвижного механизма. Труды международной научно практической конференции “КазНТУ образованию, науке и производству РК”, Алматы, 1999. - C. 358-360.

4. Иванов К.С. Парадокс механики. - ДЕП в КазГосИНТИ № 8805–КаОО, Алматы, 22.05.2000. - 12 стр

5. Иванов К.С. Теорема о равновесии замкнутого контура. - Теория механизмов и машин. Периодический научно-методический журнал. №2 (16). 2010. Том 8. Санкт-Петербургский государственный политехнический университет. -  С. 85 – 89.

6.  Иванов К.С. Оценка работоспособности бесступенчато регулируемой передачи в виде механизма с двумя степенями свободы. - Труды 2-й Международной научно-практической конференции «Машиностроение. Наука и образование». МОН РФ. Союз машиностроителей России. СПБ гос. политехнический университет. Санкт-Петербург. 14 – 15.06.2012. - С. 365 – 374.

7.  Ivanov K.S. Theory of Continuously Variable Transmission (CVT) with Two Degrees of Freedom. Paradox of mechanics. Proceedings of the American Society of Engineers Mechanics (ASME) International Mechanical Engineering Congress & Exposition (IMECE 2012). Houston, Texas, USA. 2012. - PP 543 – 562.

8.  Ivanov K.S. Discovery of the Force Adaptation Effect. -  Proceedings of the 11th World Congress in Mechanism and Machine Science. V. 2. April 1 - 4, 2004, Tianjin, China. – P. 581 - 585.

9.  Ivanov K.S. Effect of force adaptation in mechanics. - Journal of Mechanics Engineering and Automation. Vol. 1, N 3. Libertiville, USA. 2011. - P. 163 – 180.

10. Ivanov K.S. Paradox of mechanics – a basis of creation CVT. - Transactions of 2-d IFToMM Asian Conference on Mechanisms and Machines Science. November 7-10, 2012, Tokyo, Japan. - P. 245 – 264.

11. Иванов К.С., Ярославцева Е.К. Способ автоматического и непрерывного изменения крутящего момента и скорости вращения выходного вала в зависимости от сопротивления движению и устройство для его осуществления. Патент России  № 2398989 от 10 сентября 2010 г.

12. Иванов К.С., Ярославцева Е.К. Устройство передачи энергии с непрерывно переменным передаточным отношением (3 варианта). Патент Казахстана  № 023907 от 23 февраля 2011 г., 16 с.

13.  KonstantinS. Ivanov, Almaty, KZ. – Gebrauchsmusterinhaber.  Bezeichnung- Einrichtung  zur  automatischenundkontinuierichlenDrehmoment – und Drehzahlveranderung einer Abtriebswelle je nach Fahrwiderstand. Urkunde uber die Eintragung  des Gebrauchsmusters Nr. 20 2012 101 273.1. Tag der Eintragung 02.05.2012. Deutsches Patent und Markenamts. Bundesrepublik Deutschland. 2012.

Константин С. Иванов, Алматы, КАЗ - Владелец  зарегистрированного  образца. Наименование - Устройство автоматического и непрерывного изменения крутящего момента – и изменения числа оборотов  выходного вала в зависимости от сопротивления движению. Документ на регистрацию зарегистрированного образца № 20 2012 101 273.1. День Регистрации 02.05.2012. Немецкий патент и фирменное учреждение. Федеративная Республика Германия. 2012. 14 с.

14.Иванов К.С., Ярославцева Е.К., Динасылов А.Д., Шингисов Б.Т. Саморегулирующаяся адаптивная зубчатая передача ветроэнергетической установки. Патент на изобретение №  №79226. МЮ РК. Комитет по правам интеллектуальной собственности республики Казахстан. Астана. 17.10.2012. 8 с.

15. Иванов К.С., Ярославцева Е.К. Устройство передачи энергии с непрерывно переменным передаточным отношением (3 варианта). Патент Казахстана  № 023907. Астана. 23 февраля 2012 г. 16 с.

16. Ivanov K.S., Dinasylov A.D., Yaroslavseva E.K. Adaptive-Mechanical Continuously Variable Transmission. Mechanism and Machine Science. Vol. 17. New Advances in Mechanics, Transmissions and Applications. Proceedings of the Second Conference MeTrApp 2013. Springer. 2013. PP 83 – 90.

 17. Ivanov K.S., Yaroslavseva E.K. Transfer of Motion by Closed Contour: Basis of CVT. Mechanism and Machine Science. Vol. 13. Power Transmissions. Springer. 2013. PP 321 - 333.

18. Ivanov K.S. Continuously Variable Transmission: adaptive gear stepless mechanical CVT. International Conference of Gears with Exibition. VDI Wissensforum GmbH. Technical University of Munich (TUM), Garching (near Munich). Germany. 2013. PP. 984 -  987.

19. Ivanov K.S. Adaptive Robotics. Applied Mechanics and Materials. Vol. 555. ICMERA 2014. Springer. Switzerland. 2014. Springer. PP 314 - 319 .

20.  Ivanov K. S. Action of Robot with Adaptive Electric Drives of Modules. In book: Advances on Theory and Practice of Robots and Manipulators. ROMANSY 2014. Moscow. RF. Springer. 2014. PP 563 – 569.

21. Ivanov K.S. , Knol O.A., Shingissov B.T. Mechanical Adaptive Drive of Wind Turbine Generator. Proceedings of International Conference on Innovative Technologies. IN-TECH 2013. World Association of Innovative Technologies. Budapest. Hungary. 2013. PP 245-248.

22. IvanovK., Zhilisbaeva K. Concept of Drive of Sport Techniques in 21 Century.Conference on Sports Engineering and Computer Science (SECS 2014). Elsevier. AASRI. Procedia 8. London. UK.  2014. PP15 - 21.

23.  Иванов К.С. Краткая теория зубчатого вариатора. Машиностроение:сетевой электронный научный журнал. Т. 2. № 3. http: indust-engineering.ru/current-rus.html. РФ. 2014. Стр. 33 – 39.

24. Иванов К.С., Ярославцева Е.К. Теория механизмов с двумя степенями свободы. Монография. Lambert Academic Publishing. ISBN: 978-3-659-55393-6. Саарбрюкен. Германия. 2014. 171 стр.